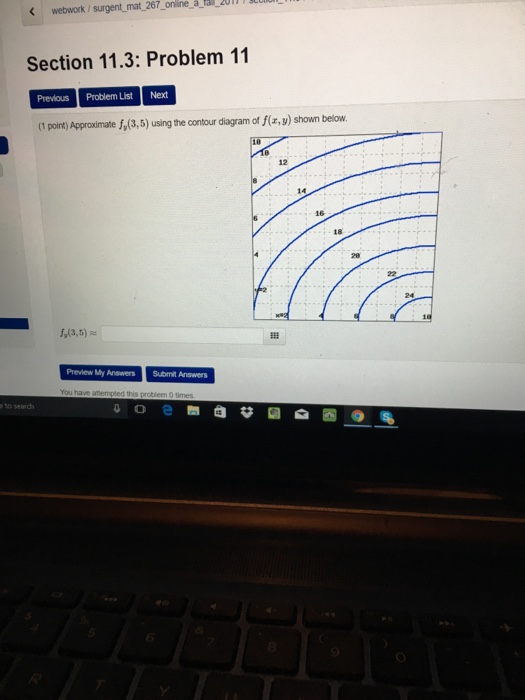
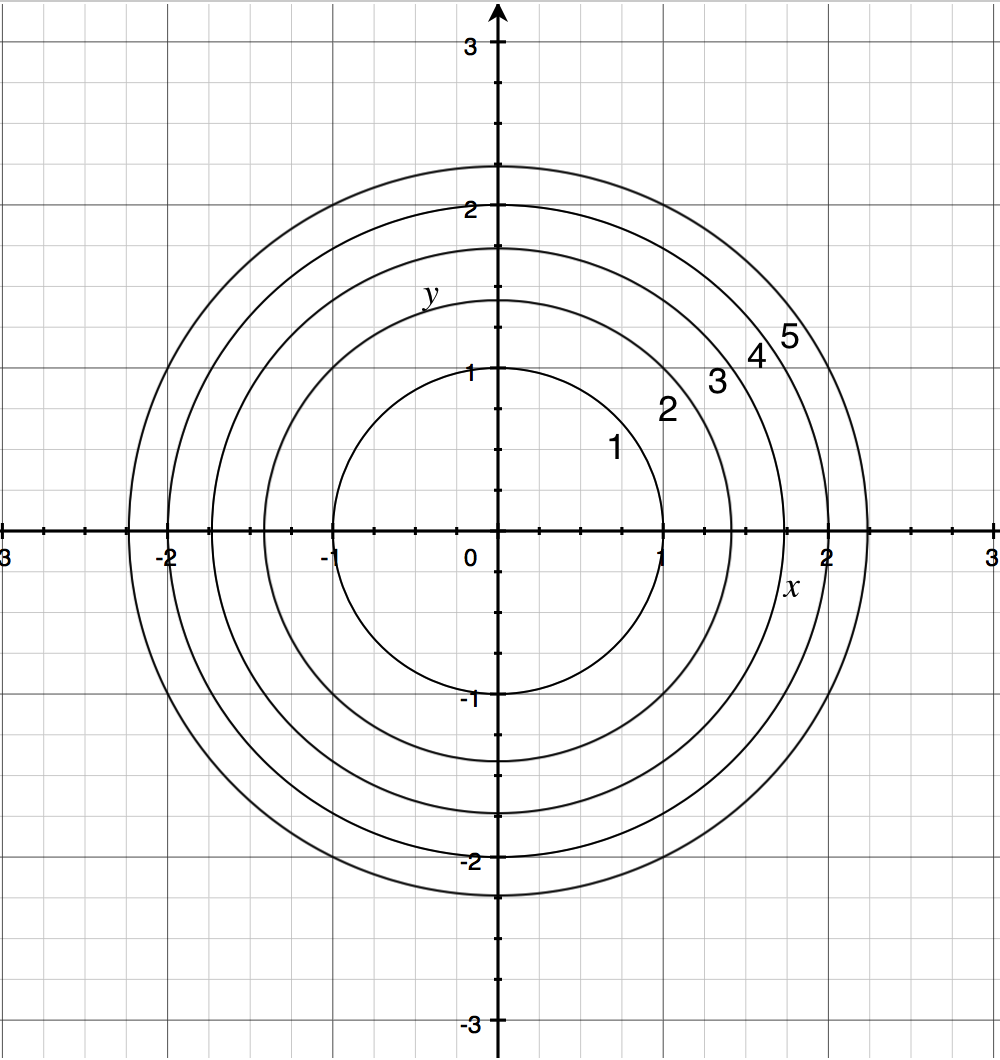
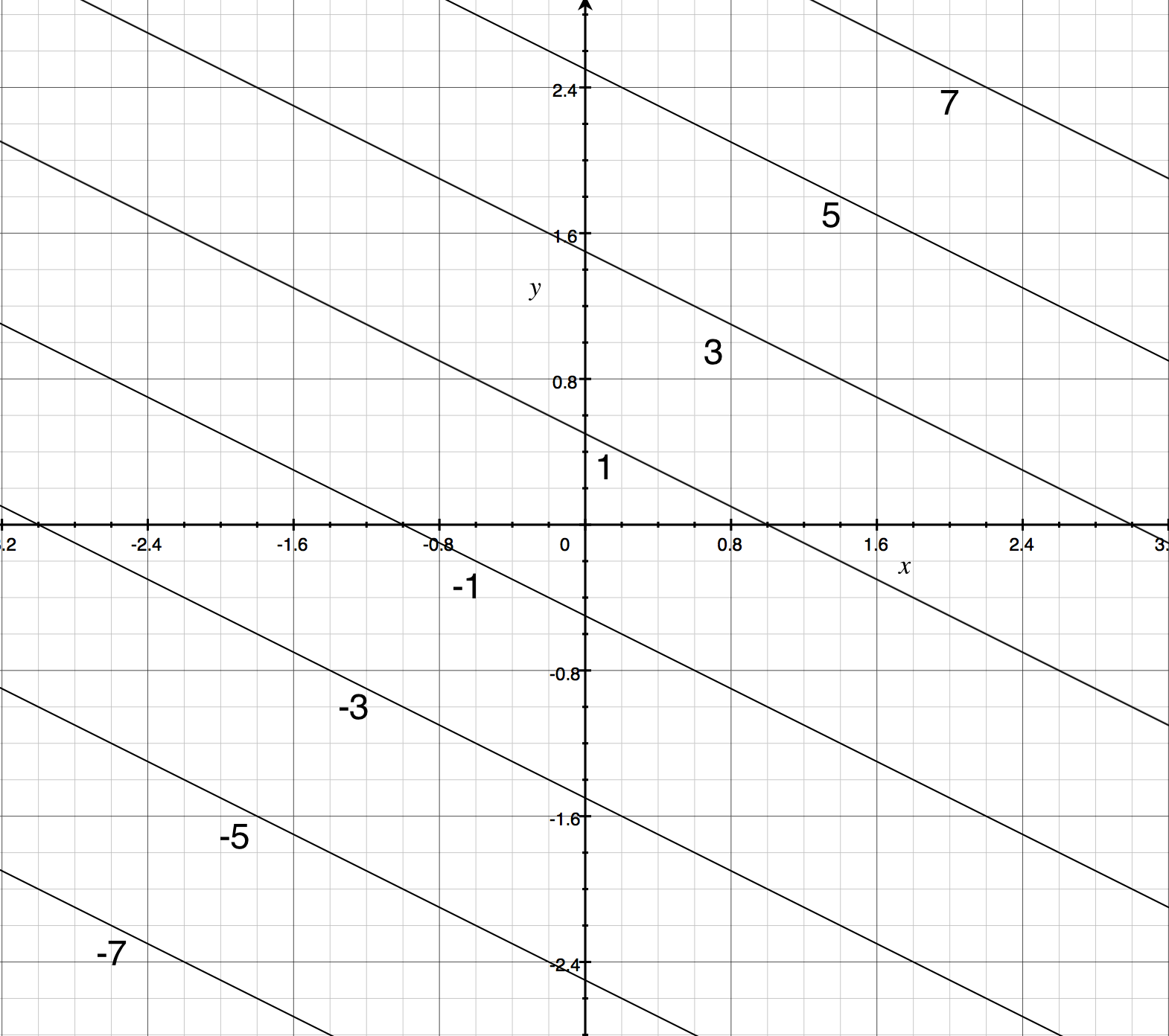
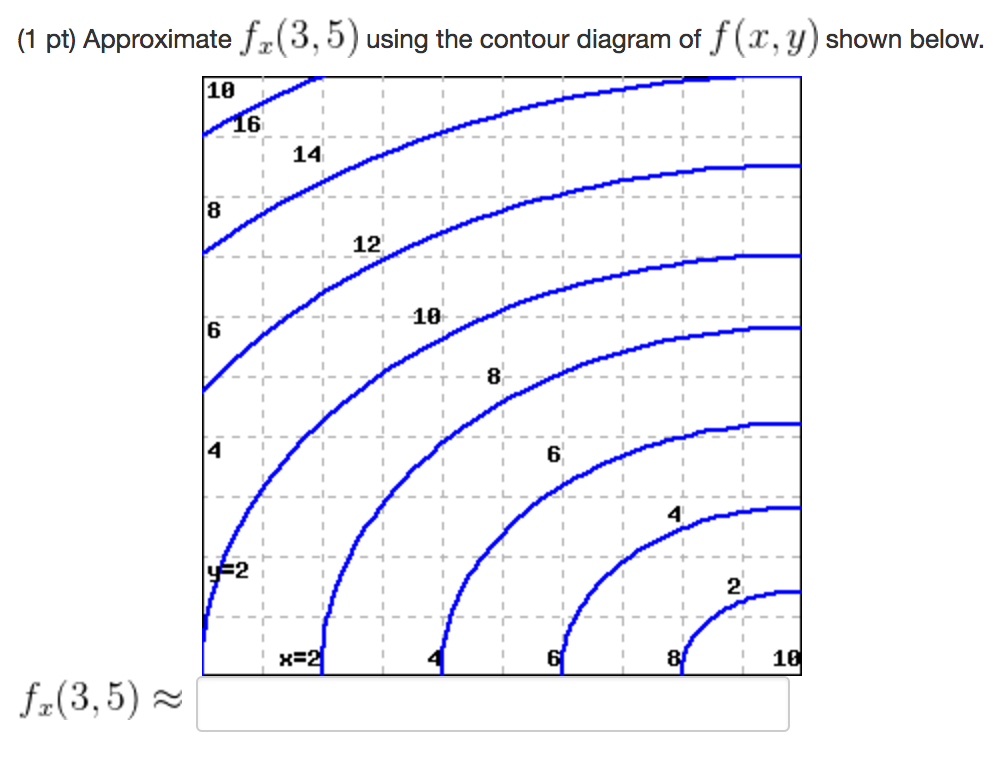
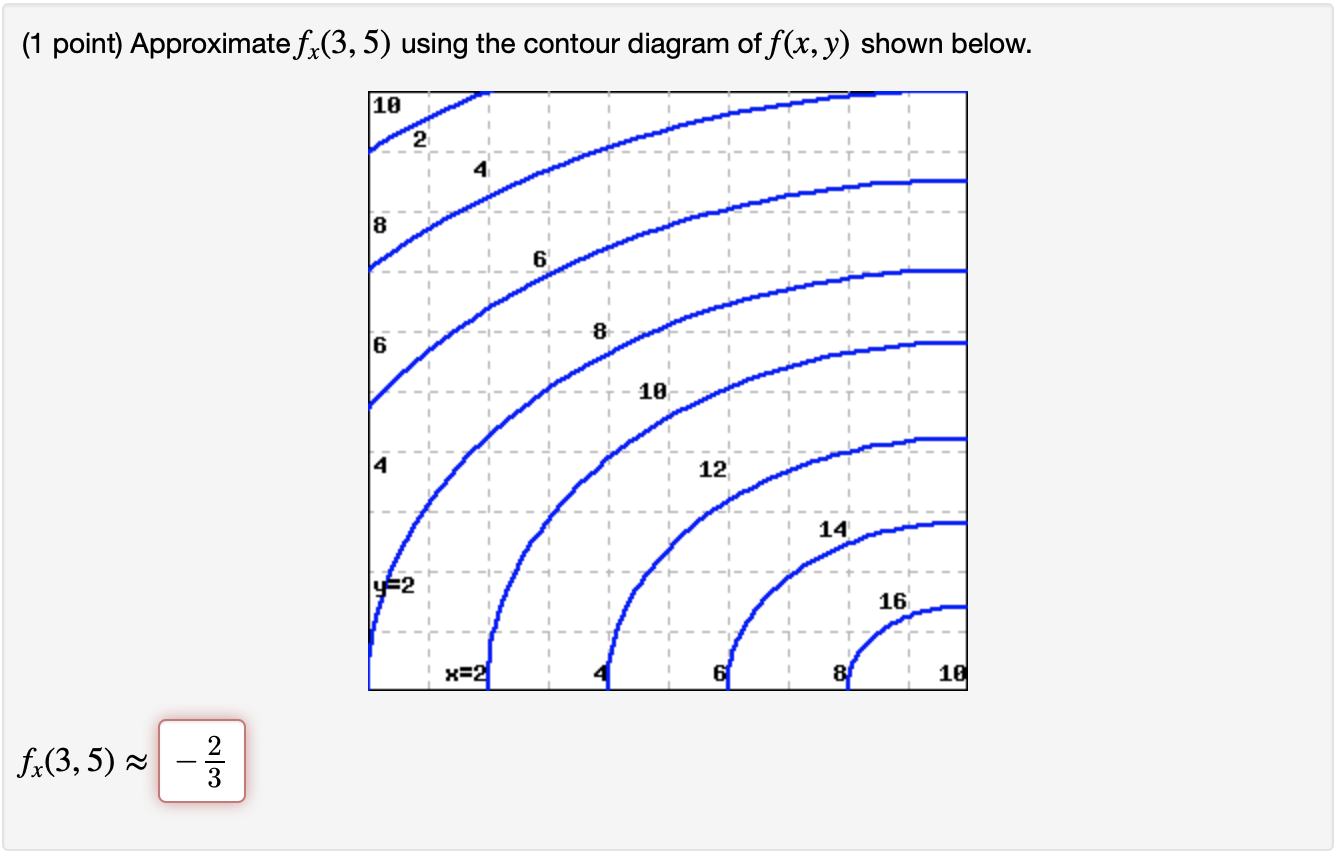
37 Approximate Fx(3,5)fx(3,5) Using The Contour Diagram Of F(x,y)f(x,y) Shown Below.

27 Tangent Planes to Level Surfaces Suppose S is a surface with equation F(x, y, z) = k, that is, it is a level surface of a function F of three variables, and let P(x 0, y 0, z 0) be a point on S. Let C be any curve that lies on the surface S and passes through the point P.Recall that the curve C is described by a continuous vector function r(t) = 〈x(t), y(t), z(t)〉. Contour maps give a way to represent the function while only drawing on the two-dimensional input space. Step 1: Start with the graph of the function. Example function graph. Step 2: Slice the graph with a few evenly-spaced level planes, each of which should be parallel to the -plane.

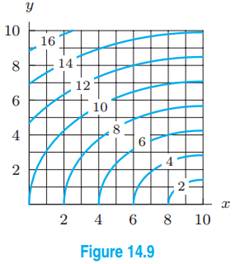
3. Let the figure below be the contour diagram of f (x,y ). Find an approximate x derivative at (2, 2) by using the centered difference quotient. Ans:1/2 4. Figure 11 shows the graph of the function P(x, 2) of x that is obtained from P(x, y) b y setting y = 2, and figure 12 shows the graph of the function P(3, y) of y that is obtained from P(x.

Approximate fx(3,5)fx(3,5) using the contour diagram of f(x,y)f(x,y) shown below.

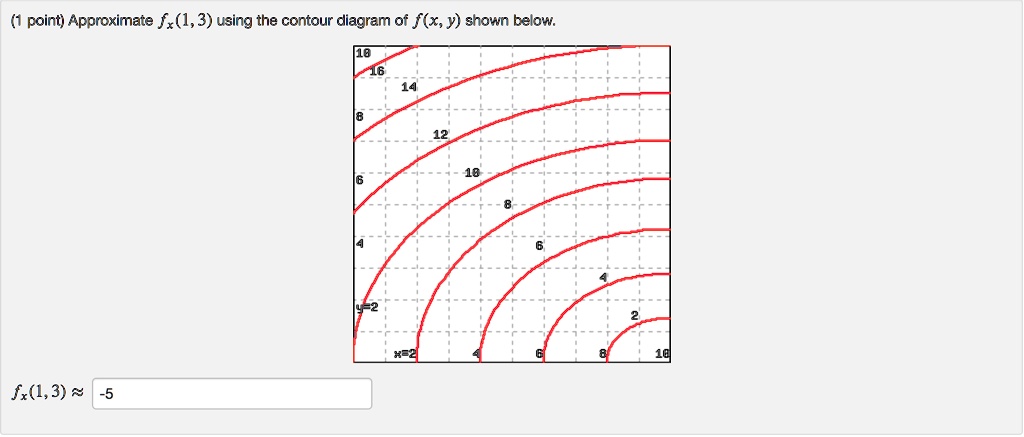
See the answer See the answer done loading. Approximate f x (1,3) using the contour diagram of f (x,y) shown below. Solve for f x (1,3) = ????? Expert Answer. Who are the experts? Experts are tested by Chegg as specialists in their subject area. We review their content and use your feedback to keep the quality high. 100% (21 ratings) We provide solutions to students. Please Use Our Service If You’re: Wishing for a unique insight into a subject matter for your subsequent individual research; fullscreen Expand. Transcribed Image Text. Approximate f (3, 5) using the contour diagram of f (x, y) shown below. 18 12 10 6 X=2 10. check_circle.

Approximate fx(3,5)fx(3,5) using the contour diagram of f(x,y)f(x,y) shown below.. Our custom writing service is a reliable solution on your academic journey that will always help you if your deadline is too tight. You fill in the order form with your basic requirements for a paper: your academic level, paper type and format, the number of pages and sources, discipline, and deadline. 4 Gradients and directional derivatives in the plane Remark 4.1. The partial derivatives f x and f y tell us the rate of change of f parallel to the coordinate axes. In this section, we consider partial derivatives 352 Chapter 14 Partial Diﬀerentiation k; in general this is called a level set; for three variables, a level set is typically a surface, called a level surface. EXAMPLE 14.1.5 Suppose the temperature at (x,y,z) is T(x,y,z) = e−(x2+y2+z2). This function has a maximum value of 1 at the origin, and tends to 0 in all directions. By using our website, you can be sure to have your personal information secured. We do not at any time disclose client’s personal information or credentials to third parties. We give anonymity and confidentiality a first priority when it comes to dealing with client’s personal information.

Overview: The partial derivatives fx(x0,y0) and fy(x0,y0) are the rates of change of z = f(x,y) at (x0,y0) in the positive x- and y-directions. Rates of change in other directions are given by directional derivatives. We open this section by deﬁning directional derivatives and then use the Chain Rule from We review their content and use your feedback to keep the quality high. Transcribed image text : Approximate f_x(3, 5) using the contour diagram of f(x, y) shown below. f_x(3, 5) 15/20 We provide solutions to students. Please Use Our Service If You’re: Wishing for a unique insight into a subject matter for your subsequent individual research; The Fill method computes the bin number corresponding to the given x, y or z argument and increments this bin by the given weight. The Fill() method returns the bin number for 1-D histograms or global bin number for 2-D and 3-D histograms.

Gradient. For a function f(x;y): gradf= rf= (f x;f y). Curl. For a vector in the plane F(x;y) = (M(x;y);N(x;y)) we de ne curlF = N x M y: NOTE. This is a scalar. In general, the curl of a vector eld is another vector eld. For vectors elds in the plane the curl is always in the bkdirection, so we simply drop the bkand make curl a scalar. 1. (1 point) Approximate f y(1;3) using the contour diagram of f(x;y) shown below. f y(1;3)ˇ Answer(s) submitted: -0.8 (correct) 2. (1 point) Find the partial derivatives indicated. Assume the variables are restricted to a domain on which the function is deﬁned. z= x5 +x y 6: ¶z ¶x = ¶z ¶y = Answer(s) submitted: 6((xˆ5+x-y)ˆ5)*(5*xˆ4. The best way to upload files is by using the “additional materials” box. Drop all the files you want your writer to use in processing your order. If you forget to attach the files when filling the order form, you can upload them by clicking on the “files” button on your personal order page. 6.041/6.431 Spring 2008 Quiz 2 Wednesday, April 16, 7:30 - 9:30 PM. SOLUTIONS. Name: Recitation Instructor: TA: Question Part

Derivative Ilmu Komputer 2 3065 P2k Unkris Ac Id

Approximate fx(3,5) using the contour diagram of fx(x,y). I am very confused full credit for right answer. Show transcribed image text (1 point) Approximate fx(3, 5) using the contour diagram of f(x, y) shown below.

Oneclass Use The Contour Diagram For F X Y Shown Below To

Week 21 Directional Derivatives And The Gradient Section 14 4

Okay, so we want to ask to meet ah the partial derivative of F with respect to X at the 0.3 comma five. And so at this point right here is Has coordinates 3:05. Now, if we want to estimate the partial derivative with respect to X, then from this point we want to move in the direction of the X axis until we arrive at the next contour line. And and so the partial derivative F with respect to X.

Ex 2 Determine A Function Value Using A Contour Map

1. f(x;y) = x+ y, x2 + y2 = 1 We use the constraint to build the constraint function, g(x;y). with f= 0. A contour diagram showing the region and contours of fis included below to illustrate the solution. 2. 5.(a)Draw contours of f(x;y) = 2x+ y for... as shown below. (b)Overlaying the constraint, we are allowed to move on a circle of radius ...

Ex Estimate The Value Of A Partial Derivative Using A Contour Map

ASSIGNMENT 6 SOLUTION JAMES MCIVOR 1. Stewart 14.3.10 [3 pts] A contour map for a function fis given. Use it to estimate f x(2;1) and f y(2;1). Solution: We can estimate f

Solved Approximate F Y 3 5 Using The Contour Diagram Of

Pt approximate f x 3 5 using the contour diagram of f. This preview shows page 4 - 5 out of 5 pages. Suppose that f(x,y)is a smooth function and that its partial derivatives have the values, fx(- 1,- 8) =4 andfy(- 1,- 8) = 3. Given thatf(- 1,- 8) = - 9, use this information to estimate the following values: Estimate of (integer value) f(- 1,- 7.

Chapter 10 Numerical Solution Methods For Engineering Analysis

3 3. Determine the sign of f x and f y at the point using the contour diagram of f in the gure below. (a) P (b) Q (c) R (d) S 4. Approximate f x(3;5) using the contour diagram of f(x;y) shown in the gure below.

Lecture Notes1 Microeconomic Theory

Approximate f x 3 5 using the contour diagram of f x. This preview shows page 4 - 5 out of 5 pages. y0)h. Here, we have f(3,5)≈8, and f(6,5)≈ 6. Thus, we can take fx≈ f(6,5)- f(3,5) 3 = 6- 8 3 = - 0.666667. Of course, we could takeh < 0 and use the contour f= 6 as well, or average the two results.Answer (s) submitted: • -2/3 (correct.

Approximate F X 3 5 Using The Contour Diagram Of F X Y Shown

318 Chapter 4 Fourier Series and Integrals Zero comes quickly if we integrate cosmxdx = sinmx m π 0 =0−0. So we use this: Product of sines sinnx sinkx= 1 2 cos(n−k)x− 1 2 cos(n+k)x. (4) Integrating cosmx with m = n−k and m = n+k proves orthogonality of the sines.

Contour Map Of F X Y 1 X 2 Y 2

fullscreen Expand. Transcribed Image Text. Approximate f (3, 5) using the contour diagram of f (x, y) shown below. 18 12 10 6 X=2 10. check_circle.

Partial Derivatives

Solution Manual - Fluid Mechanics 4th Edition - Frank M. White

Problem 6 1 Point Use The Contour Diagram Of F In The

This video explains how to use the slope of a secant line to determine the value of a partial derivative using a contour map.Site: http://mathispower4u

Solved Point Approximate F X 1 3 Using The Contour Diagram

Enter the email address you signed up with and we'll email you a reset link.

Get Answer Approximate F X 3 5 Using The Contour

subject to the constraint 2x2 +(y 1)2 18: Solution: We check for the critical points in the interior f x = 2x;f y = 2(y+1) =)(0; 1) is a critical point : The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum with

Matlab Tutorial

hf = 4 C f L u 2/2gd = 4 x 0.0083 x 25000 x 2.4114 2/(2 x 9.91 x 0.08) = 3075 m 2. Water flows in a pipe at 0.015 m 3/s. The pipe is 50 mm bore diamet er. The pressure drop is 13 420 Pa per metre length. The density is 1000 kg/m 3 and the dynamic viscosity is 0.001 N s/m 2. Determine i. the wall shear stress (167.75 Pa) ii. the dynamic pressure.

Lubricants Free Full Text Improvement In The Hard Milling

Functions & Graphing Calculator. \square! \square!. Get step-by-step solutions from expert tutors as fast as 15-30 minutes. Your first 5 questions are on us!

Answer The Following Questions For The Given Contour Diagram

Once again, the derivative gives the slope of the tangent line shown on the right in Figure 10.2.3.Thinking of the derivative as an instantaneous rate of change, we expect that the range of the projectile increases by 509.5 feet for every radian we increase the launch angle $y$ if we keep the initial speed of the projectile constant at 150 feet per second.

Multivariable Calculus 1 A Function F X Y

If f(x) is the density function for a random variable X, then we can represent y f(x) graphically by a curve as in Fig. 2-2. Since f(x) 0, the curve cannot fall below the x axis. The entire area bounded by the curve and the x axis must be 1 because of Property 2 on page 36. Geometrically the probability that X is between a and b, i.e.,

Contour Maps Article Khan Academy

If the following is a contour diagram for f(x,y) with the z = 0 contour at the origin, going up by 1 for each concentric circle, approximate the rate of change of f(x,y) at (1,1) in the direction of

Multivariable Calculus Question 3 2 Pts The Contour

Beyond simple math and grouping (like "(x+2)(x-4)"), there are some functions you can use as well. Look below to see them all. They are mostly standard functions written as you might expect. You can also use "pi" and "e" as their respective constants. Please note: You should not use fractional exponents.

Contour Maps Article Khan Academy

Answer to 16. (1 point) Approximate fr(3,5) using the contour diagram of f(x,y) shown below. 10 14 12 10 2 *=2 of 10 fx (3, 5) ~

Approximate F X 3 5 Using The Contour Diagram Of F X Y Shown

Approximate fx(3,5) using the contour diagram of f(x,y) shown below. fx(3,5)?. What happens next? After payment, your answer will be immediately delivered to your email (so don't forget to check your spam folder in case you don't see anything!)