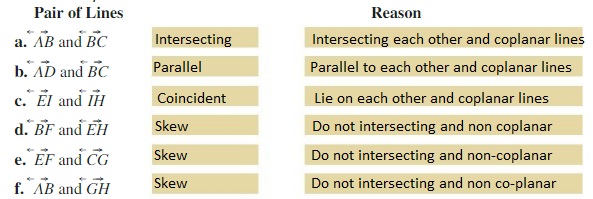
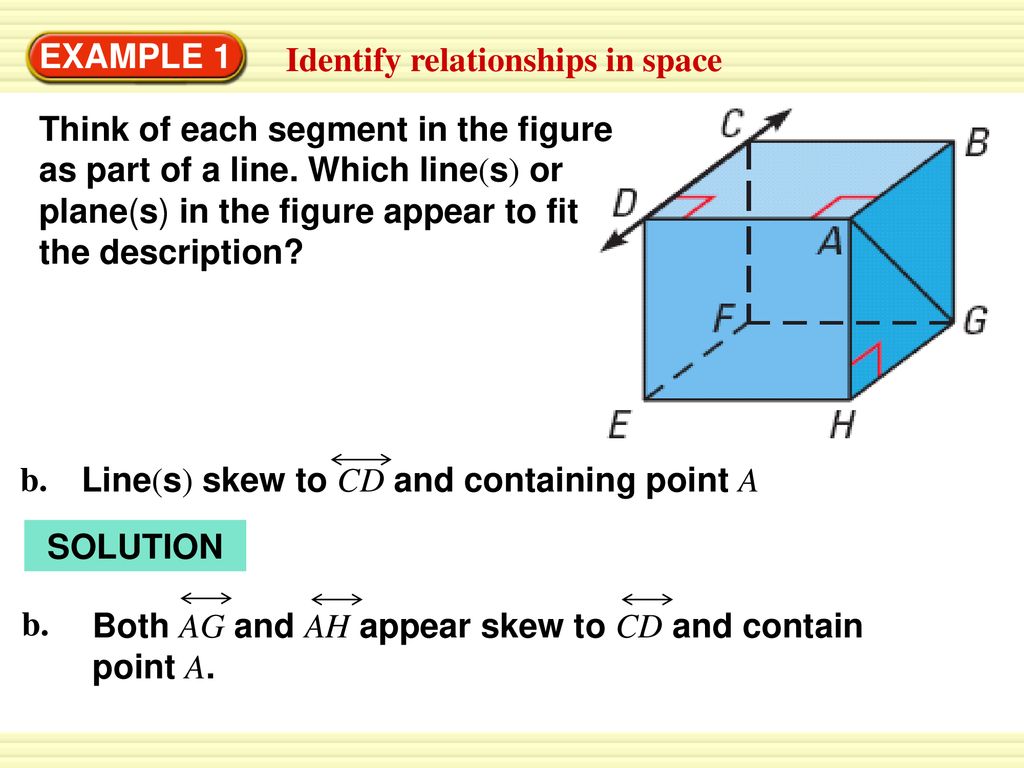
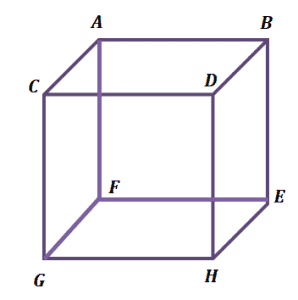
39 Consider The Diagram. Lines A And D Are Non-coplanar. Parallel. Perpendicular. Skew.

Consider the diagram lines a and d are non coplanar parallel perpendicular skew. Log in join now secondary school. Ask for details. Log in join now 1. Lines a and c are coplanar. Follow report by maddylopez1027 17032019 log in to add a. Get the answers you need now. P is a point on the perpendicular bisector i of mn. none of these. skew. perpendicular. Planes Q and R are parallel. Explain how you know lines a and b are skew. Skew lines are noncoplanar and do not intersect. Line a lies in plane Q and line b lies in plane R, so the lines are not coplanar. No other plane can be drawn through the lines, so they are not parallel. So, a and b are skew.

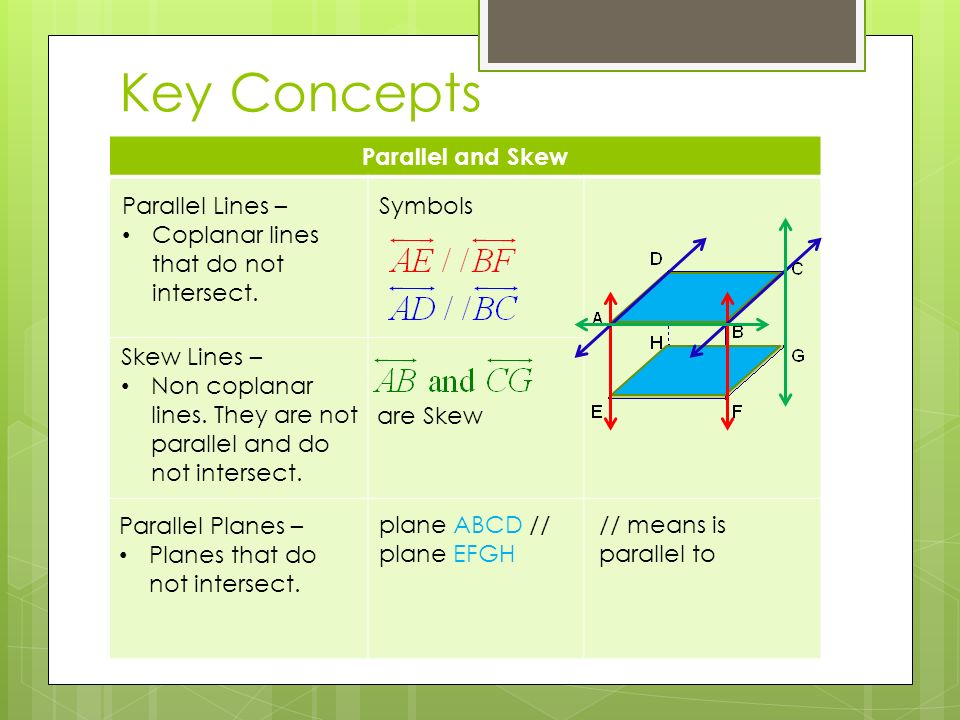
Skew lines are lines that are non-coplanar and do not intersect. Two planes are parallel if they never intersect. Two planes are perpendicular if they intersect and form a right angle. Example: Identify 3 pairs of parallel planes. Identify 2 pairs of perpendicular planes. Identify 2 pairs of skew lines.

Consider the diagram. lines a and d are non-coplanar. parallel. perpendicular. skew.

Skew lines perpendicular parallel lines planes intersecting lines transversals duration. Consider the diagram lines a and d are non coplanar parallel perpendicular skew. So a and b are skew. Skew lines are lines that are non coplanar and do not intersect. Coplanar lines that do not intersect are parallel. Two planes are parallel if they never. 60 seconds. Report an issue. Q. Why are lines AC and RS skew lines? answer choices. They lie in different planes and will never intersect. They lie in the same plane but will never intersect. They lie in different planes but will intersect if a plane is drawn to contain both lines. They lie in different planes and will be parallel if a plane is. Consider the diagram. Why are lines e and c skew lines? They lie in different planes and will never intersect. They lie in the same plane but will never intersect. They lie in different planes but will intersect if a plane is drawn to contain both lines. They lie in different planes and will be parallel if a plane is drawn to contain both lines.

Consider the diagram. lines a and d are non-coplanar. parallel. perpendicular. skew.. As shown in the three examples, as long as the lines are not coplanar, do not intersect, and are not parallel, they can be considered skew lines. Example 6 Take a screenshot or snip the image below and sketch one line that will still be skew with the two other lines. Plane Q contains line a. Plane R contains line b. If a third plane could be drawn which contains both lines a and b, then. lines a and b must be parallel. lines a and b cannot be parallel. lines a and b must be skew. lines a and b must be perpendicular. lines a and b must be parallel. Consider the diagram. Skew lines : If two lines lie on different plane and do not intersect each other, then they are called skew lines. From the given figure it is clear that lines a and d lie on the same plane M and form right angle. So, lines a and d are perpendicular. Therefore, the correct option is C. Step-by-step explanation: A non coplanar line is when two different points are in a different plane, as we can see, a is on a vertical axis, while d is a horizontal axis, two completely different planes, fitting a non coplanar answer. jd3sp4o0y and 2 more users found this answer helpful.

Consider the incomplete paragraph proof. Given: P is a point on the perpendicular bisector, l, of MN. Prove: PM = PN Because of the unique line postulate, we can draw unique line segment PM. Using the definition of reflection, PM can be reflected over line l. Lines a and c are. Consider the diagram lines a and d are. Lines a and c are coplanar. Skew lines are noncoplanar and do not intersect. Plane x contains line b. So a and b are skew. Parallel perpendicular lines. No other plane can be drawn through the lines so they are not parallel. If the dashed line at 1 atm of pressure is followed from 100. Ixl Identify Parallel Perpendicular And Skew Lines And Planes Answer to consider the diagram. Consider the diagram lines a and d are non coplanar parallel perpendicular skew. Skew lines are noncoplanar lines that do not intersect. If two lines that do not meet are not coplanar they are called skew lines. Consider the incomplete paragraph proof. Given: P is a point on the perpendicular bisector, l, of MN. Prove: PM = PN Because of the unique line postulate, we can draw unique line segment PM. Using the definition of reflection, PM can be reflected over line l.

Perpendicular lines are intersecting lines that meet at right angles and transversals are lines that intersect with two or more parallel lines. Consider the diagram lines a and d are non coplanar parallel perpendicular skew. Skew lines are noncoplanar lines that do not intersect. Two planes are perpendicular if they intersect and form a right. Skew lines : If two lines lie on different plane and do not intersect each other, then they are called skew lines. From the given figure it is clear that lines a and d lie on the same plane M and form right angle. So, lines a and d are perpendicular. Therefore, the correct option is C. douwdek0 and 68 more users found this answer helpful. In Exercises 16—19, use the diagram. 16. Name a point that is coplanar with points A, D, and G. 17. Name the intersection of plane HEG and plane DFE. 18. Name a point that is collinear with BH. 19. Name a point that is not coplanar with points C, E, and M. 20. What geometric terms are modeled by the Eiffel Tower? line Example: In the diagram above, points A, B, and C are collinear and lie in plane M so, they are collinear and coplanar (you can draw infinitely many planes containing line AB).Points A, B, C, and D lie in plane M so are coplanar but not collinear since they do not lie on the same line.

Chapter 3 Angles And Lines Mathematics Quizizz

Are skew lines perpendicular. Consider the diagram lines a and d are non coplanar parallel perpendicular skew. Start studying geometry ch. Parallel lines are two lines in the same plane that never intersect. Because of the unique line postulate we can draw unique line segment pm. Lines a and d are.

What Are Coplanar Points Definition Amp Examples Video

Consider the diagram. Why are lines e and c skew lines? They lie in different planes and will never intersect. They lie in the same plane but will never intersect. They lie in different planes but will intersect if a plane is drawn to contain both lines. They lie in different planes and will be parallel if a plane is drawn to contain both lines.

$Big Ideas Math Geometry Answers Chapter 3 Parallel And - Consider the diagram. lines a and d are non-coplanar. parallel. perpendicular. skew.$

Big Ideas Math Geometry Answers Chapter 3 Parallel And

Consider the diagram. lines a and d are. Consider the diagram lines a and d are. It should go all the way to the edges of the table as shown. Use the diagram to state the theorem definition postulate or property that justifies the given statement a b c 180. Consider the incomplete paragraph proof. Transversal ef cuts parallel lines ab and cd as.

Lines A And D Are A Non Coplanar B Parallel C

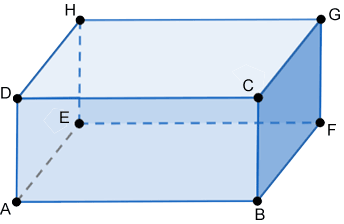
Consider the diagram. planes m and n intersect at line d. lines a, b, and e are on plane m. line a is vertical and forms a right angle with line d. line b is diagonal and goes up and to the right. line e is at the top of the plane and is close to being horizontal. line c is on plane n and goes slightly up and to the right. lines a and d are non-coplanar. parallel. perpendicular. skew.

Points Lines Planes Segments Amp Rays Collinear Vs Coplanar Points Geometry

Correct answers: 2 question: Consider the diagram. Planes M and N intersect at line d. Lines a, b, and e are on plane M. Line a is vertical and forms a right angle with line d. Line b is diagonal and goes up and to the right. Line e is at the top of the plane and is close to being horizontal. Line c is on plane N and goes slightly up and to the right. Lines a and d are non-coplanar. parallel.

Parallel And Perpendicular Lines Lesson West Orange Stark

Sensors Free Full Text Vision Based Building Seismic

60 seconds. Report an issue. Q. Why are lines AC and RS skew lines? answer choices. They lie in different planes and will never intersect. They lie in the same plane but will never intersect. They lie in different planes but will intersect if a plane is drawn to contain both lines. They lie in different planes and will be parallel if a plane is.

Lines A And D Are Non Coplanar Parallel Perpendicular Skew

Answer (1 of 5): You can draw two perpendicular lines that are non-coplanar. Consider the line from (0,0,0) to (1,0,0) and the line from (0,0,1) to (0,1,0). Normally when you consider orthogonality, you're considering vectors that originate from the same point (i.e., have a common origin, or com...

$Coplanar - Consider the diagram. lines a and d are non-coplanar. parallel. perpendicular. skew.$

Coplanar

Parallel lines must be coplanar. Consider the diagram lines a and d are non coplanar parallel perpendicular skew. Because of the unique line postulate we can draw unique line segment pm. Keep me logged in. Views view upvoters. Would you call the non coplanar lines perpendicular. If two lines intersect and form a right angle the lines are.