38 in the diagram below de df and ef are midsegments of abc
16 In the diagram below, DE, DF, and EF are midsegments of ABC. The perimeter of quadrilateral ADEF is equivalent to 1) AB +BC +AC 2) 1 2 AB+ 1 2 AC 3) 2AB +2AC 4) AB +AC 17 Under which transformation would A'B'C', the image of ABC, not be congruent to ABC? 1) reflection over the y-axis 2) rotation of 90° clockwise about the origin segment ABC are A(−8,7) and C(7,−13). If AB:BC =3:2, the coordinates of B are 35 In the diagram below, ABC ∼ DEC. If AC =12, DC =7, DE =5, and the perimeter of ABC is 30, what is the perimeter of DEC? 36 In the diagram below, DE, DF, and EF are midsegments of ABC. The perimeter of quadrilateral ADEF is equivalent to
4 In the diagram below, DE, DF, and EF are midsegments of L.ABC. B A c The perimeter of quadrilateral ADEF is equivalent to (1) AB + BC +AC (2) _!_AB+ _!_AC 2 2 (3) 2AB + 2AC ®AB+AC 5 In the diagram below, if L.ABE ~ L.CDF and AEFC is drawn, then it could be proven that quadrilateral ABCD is a (1) square (2) rhombus (3) rectangle

In the diagram below de df and ef are midsegments of abc
11 In the diagram below, DE, DF, and EF are midsegments of ABC. The perimeter of quadrilateral ADEF is equivalent to 1) AB +BC +AC 2) 1 2 AB+ 1 2 AC 3) 2AB +2AC 4) AB +AC 12 In the two distinct acute triangles ABC and DEF, ∠B ≅∠E. Triangles ABC and DEF are congruent when there is a sequence of rigid motions that maps 1) ∠A onto ∠D, and ∠C onto ∠F 2) AC onto DF, and BC onto EF 3) ∠C onto ∠F, and BC onto EF 4 In the diagram below, DE DF and EF are midsegments of AABC. The perimeter of is equivalent to (l) AB + BC + AC (2) -AB + -AC (3) 2AB + 2AC 5 In the diagram below, if AABE ACDF and AEFC is drawn, then it could be proven that quadrilateral ABCD is a (l) square (2) rhombus (3) rectangle (4) parallelogram opp. sues BOTH [OVER] In Exercises 3–6, use the graph of ABC with midsegments DE —, EF —, and DF — . (See Example 1.) x y 2 −6 −2 −6 2 A B C D F E 3. Find the coordinates of points D, E, and F. 4. Show that DE — is parallel to CB — and that DE = 1— 2 CB. 5. Show that EF — is parallel to AC — and that EF = 1— 2 AC. 6. Show that DF —
In the diagram below de df and ef are midsegments of abc. In Exercises 3–6, use the graph of ABC with midsegments DE —, EF —, and DF — . (See Example 1.) x y 2 −6 −2 −6 2 A B C D F E 3. Find the coordinates of points D, E, and F. 4. Show that DE — is parallel to CB — and that DE = 1— 2 CB. 5. Show that EF — is parallel to AC — and that EF = 1— 2 AC. 6. Show that DF — 4 In the diagram below, DE DF and EF are midsegments of AABC. The perimeter of is equivalent to (l) AB + BC + AC (2) -AB + -AC (3) 2AB + 2AC 5 In the diagram below, if AABE ACDF and AEFC is drawn, then it could be proven that quadrilateral ABCD is a (l) square (2) rhombus (3) rectangle (4) parallelogram opp. sues BOTH [OVER] 11 In the diagram below, DE, DF, and EF are midsegments of ABC. The perimeter of quadrilateral ADEF is equivalent to 1) AB +BC +AC 2) 1 2 AB+ 1 2 AC 3) 2AB +2AC 4) AB +AC 12 In the two distinct acute triangles ABC and DEF, ∠B ≅∠E. Triangles ABC and DEF are congruent when there is a sequence of rigid motions that maps 1) ∠A onto ∠D, and ∠C onto ∠F 2) AC onto DF, and BC onto EF 3) ∠C onto ∠F, and BC onto EF



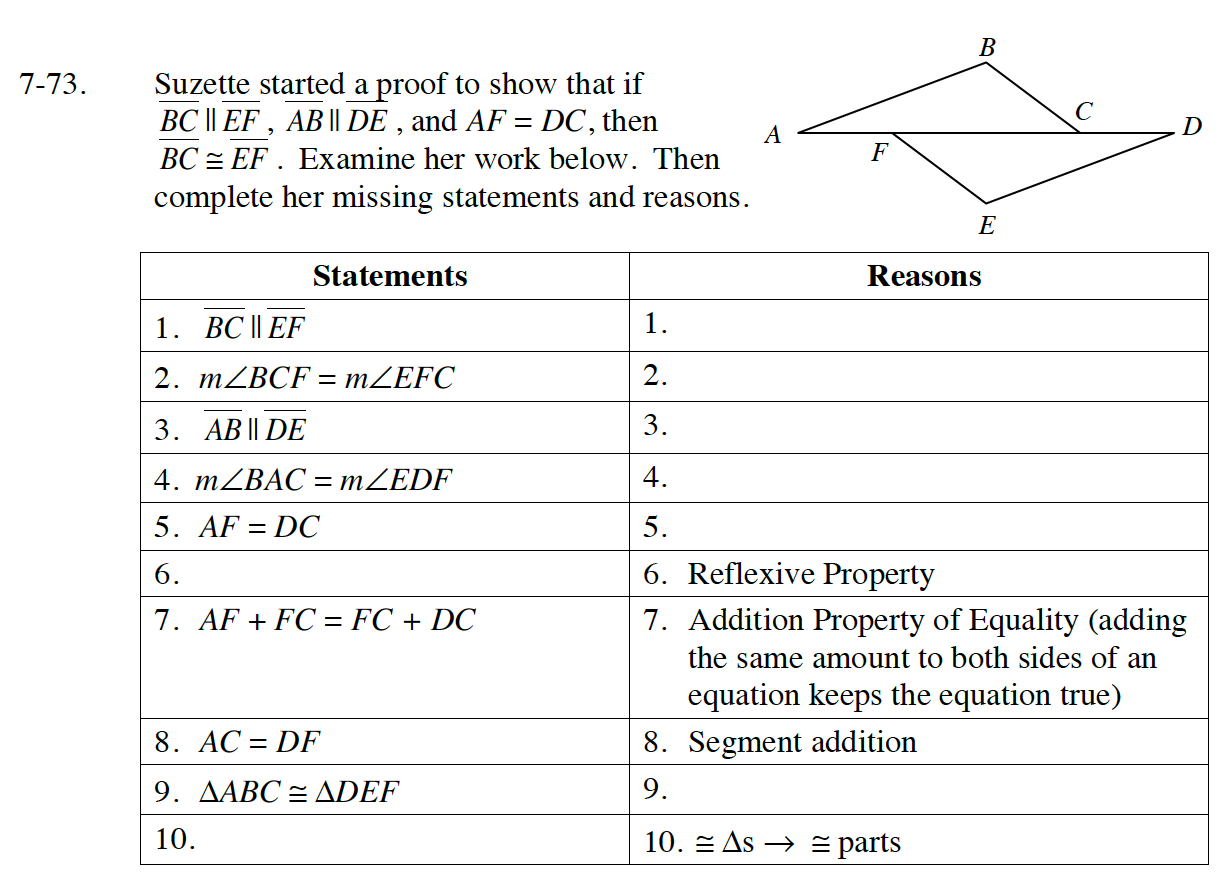


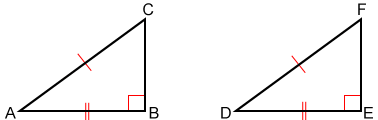

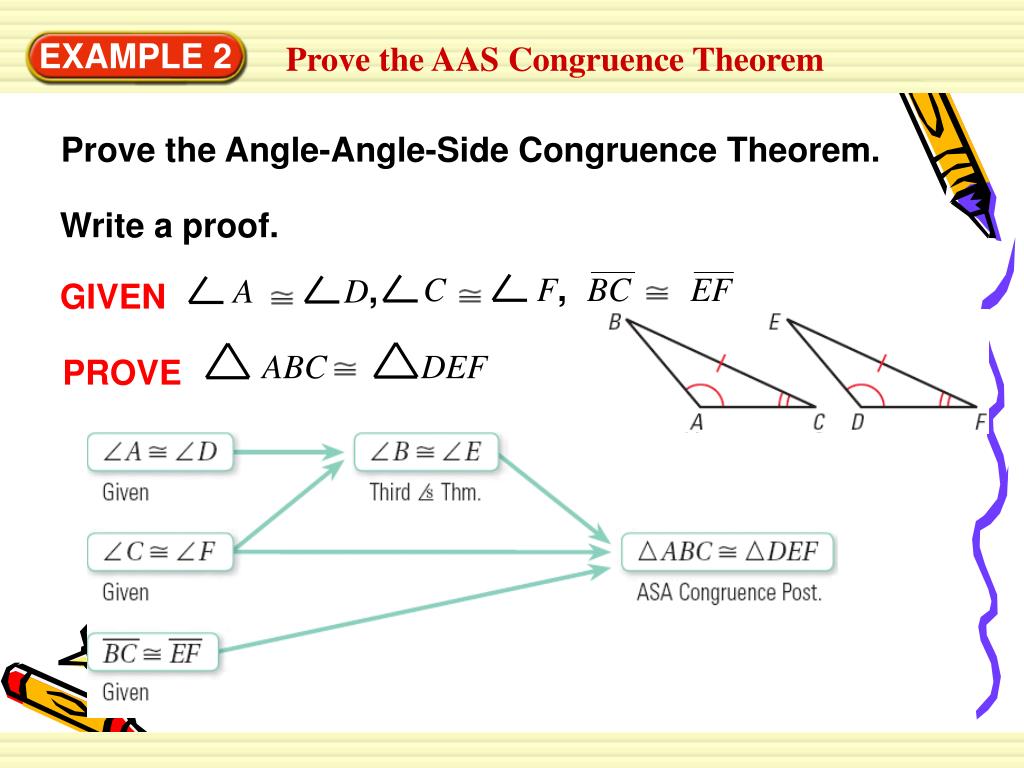










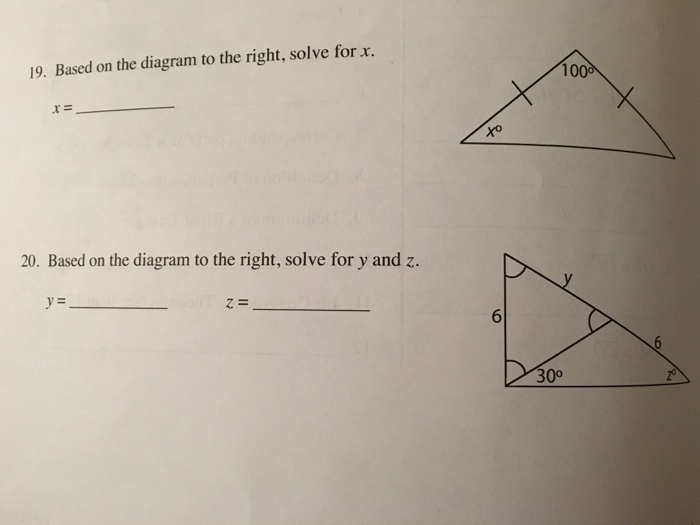



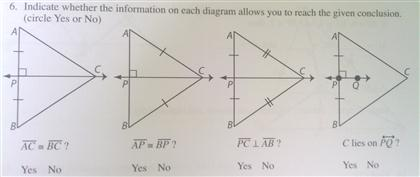
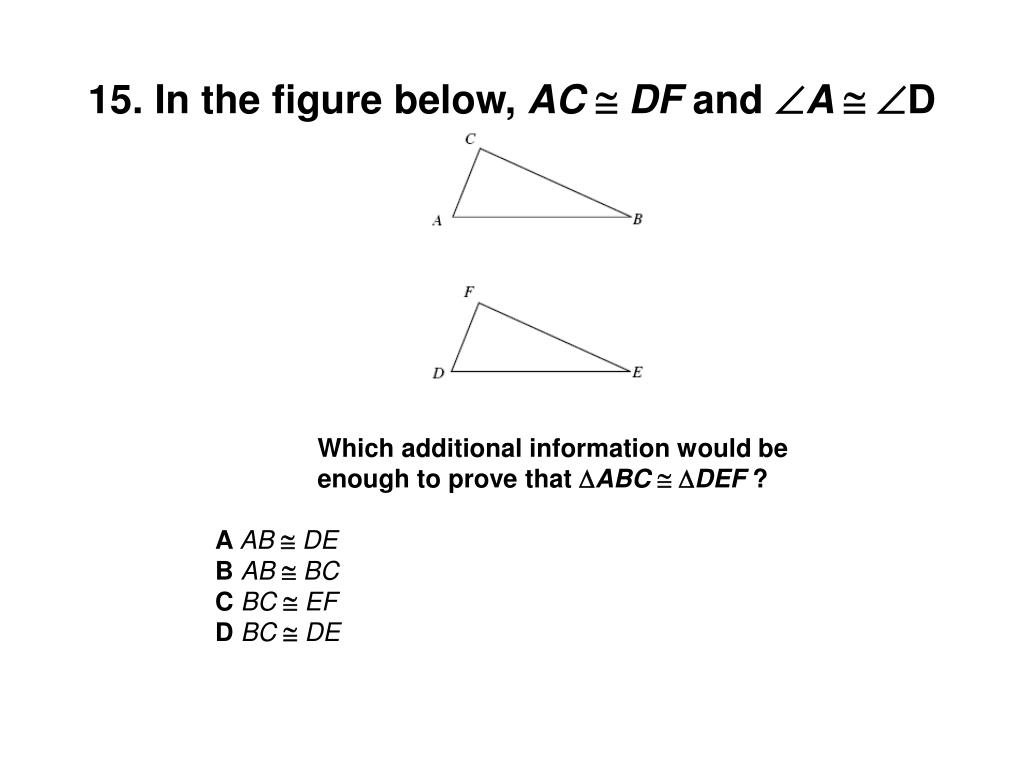




0 Response to "38 in the diagram below de df and ef are midsegments of abc"
Post a Comment